Alex Robotics
Intro DAP Guide Notes Vidéos
sky

GRO860

Apprentissage par renforcement et commande optimale

Pourquoi ce cours?

  • Comprendre les fondements de l’apprentissage par renforcement et la commande optimale
  • Faire les liens avec la science des asservissements;
  • Apprendre à utiliser des algorithmes pour synthétiser des politiques optimales

Du choix des forces dans un robot jusqu'au choix de la pièce à déplacer dans un jeu d'échec.

Quoi?

  • Principe d’optimalité: Équations de Bellman, fonction coût/récompense, contraintes, etc.
  • Modèle d’évolution: Équations différentielles, Chaînes de Markov, Échantillonnage.
  • Techniques de solution: Programmation dynamique, LQR, Apprentissage par Renforcement.

Quand et où?

Cours à option à l'université de sherbrooke : GRO860 . La version automne 2024 sera les lundi 13h-16h en salle à déterminer.

Vidéo de présentation du cours

Matériel

Guide
Notes de cours
Vidéos

Introduction

Une approche unifiée pour la science de la prise de decision en temps réel.

Le but du cours est de faire le lien entre le domaine des asservissements et les algorithmes de décision basé sur l’IA. Le cours présentera les outils pour vous permettre de de traduire un problème de décisions en temps réel sous la représentation mathématique adapté pour synthétiser et optimiser une politique de décision, avec des applications dans plusieurs domaines de la robotique à la finance.

Ce cours présente les approches pour prendre des décisions intelligentes sous un cadre théorique unifié basé sur le principe de la programmation dynamique. Il vise d'abord a établir les liens entre les approches issues du domaine de l'ingénierie (la science des asservissements et la commande optimale) et les approches issues des sciences informatiques (recherche opérationnelle et l'apprentissage par renforcement) qui ont en fait les même bases mathématiques. Il vise principalement à donner à un lecteur issue du domaine de l'ingénierie les bases pour comprendre et utiliser les approches numériques issues des sciences informatiques, comme l'apprentissage par renforcement, qui permettent de calculer des politiques décisionnelles optimales.

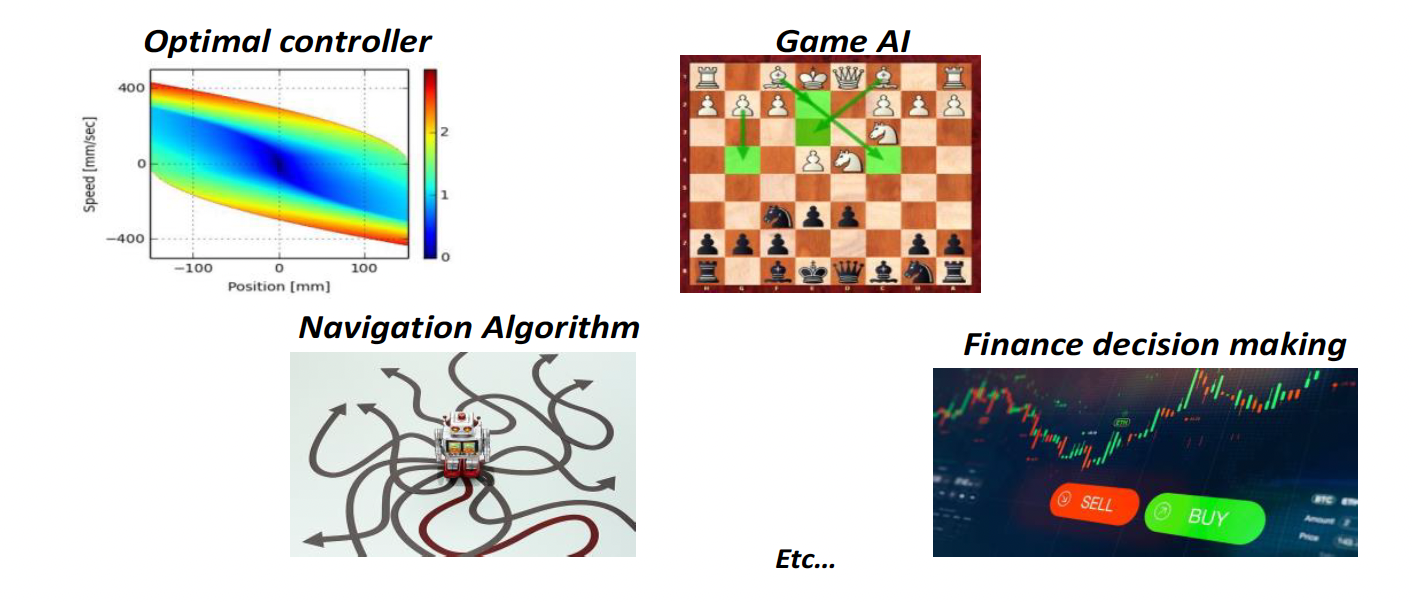
Plusieurs problèmes en apparence très différents, sont en fait des problèmes qu'on peut analyser et résoudre avec les mêmes outils mathématiques

Contenu détaillé du cours

Semaines Sujets Travaux
1

Introduction

  • Programmation dynamique
  • Applications et exemples (contrôle, navigation, finance, game AI, etc.)
2 à 8

Principe d’optimalité

  • Fonction de coût, contraintes et objectifs
  • Équations de Bellman
  • Équation HJB
  • Solution analytique pour les systèmes linéaires avec un coût quadratique (LQR)
  • Formulation MiniMax pour le contrôle robuste
  • Formulation Probabiliste
 Devoirs papier/crayon + devoirs de code (Python)
2 à 8

Modélisation

  • États discrets vs états continus
  • Temps discret vs temps continus
  • Évolution déterministe vs évolution stochastique
  • Modèle d’état; Équation différentielles; Équation de différences; Chaînes de Markov;
  • Graphiques de transitions;
 Devoirs papier/crayon + devoirs de code (Python)
2 à 8

Méthode de synthèse / apprentissage

  • Méthodes hors-ligne
    • Itération de valeur (value iteration)
    • Itération de loi de commande (policy iteration)
  • Apprentissage par renforcement
    • Différence temporelle
    • Q-Learning
    • Policy gradient
 Devoirs papier/crayon + devoirs de code (Python)
8 à 12

Méthodes avancées

  • Approximation de fonctions
  • Deep-reinforcement learning

Projet de session

  • Un projet au choix de l'étudiant impliquant des notions du cours.
  • L’évaluation du projet consistera en une présentation finale devant la classe